Single Input Modules
Single Input Modules (SIM) are a motif family in transcription networks where a master transcription factor \(X\) controls a group of target genes \(Z_1, Z_2, \ldots, Z_n\), each of which only takes \(X\) as input. \(X\) regulates all the genes in the same way (either activation or repression) and is usually autoregulatory. The target genes in a SIM typically share a common biological function.
LIFO temporal programs with SIMs
SIMs can generate temporal programs of expression, activating the target genes in a precise order, defined by their binding affinities.
include("GeneticCircuits.jl")
t_on = [0.0]
t_off = [7.5]
steppulse(t,a,b) = Θ(t,a)*(1-Θ(t,b))
SX(t,t_on,t_off) = sum( map(τ -> steppulse(t,τ[1],τ[2]), zip(t_on,t_off)) )
N = 3 # number of output genes
@parameters S Kx αx Kz[1:N] αz[1:N]
@variables t X(t) (Z(t))[1:N]
rx = Reaction[]
for i in 1:N
push!(rx,
# 0 → Zᵢ with rate Θ(X>Kzᵢ)
Reaction(Θ(X,Kz[i]), nothing, [Z[i]]),
# Zᵢ → 0 with rate αzᵢ
Reaction(αz[i], [Z[i]], nothing)
)
end # for
push!(rx,
# 0 → X with rate S
Reaction(S, nothing, [X]),
# X → 0 with rate αx
Reaction(αx, [X], nothing)
)
rn = ReactionSystem(rx, t,
[X; collect(Z)],
[S; Kx; αx; collect(Kz); collect(αz)],
name=:SIM_LIFO
)
p = [
S => 0.0,
αx => 1.0, Kx => 0.5,
Pair.(collect(Kz), range(0,1;length=N+3)[3:end-1])...,
Pair.(collect(αz), 1.0)...
]
u₀ = [X => 0.0; Pair.(collect(Z), 0.0)]
tspan = (-1.0, 15.0)
S_on!(integrator) = integrator.p[1] = 1.0
S_off!(integrator) = integrator.p[1] = 0.0
cb_on = PresetTimeCallback(t_on, S_on!)
cb_off = PresetTimeCallback(t_off, S_off!)
cb = CallbackSet(cb_on, cb_off)
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Rosenbrock23(), callback=cb)
plot(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="S(t)", leg=:topright)
plot!(sol, idxs=(0,1))
plot!(sol, idxs=(0,2:N+1), lab="Z".*["₁" "₂" "₃"].*"(t)")
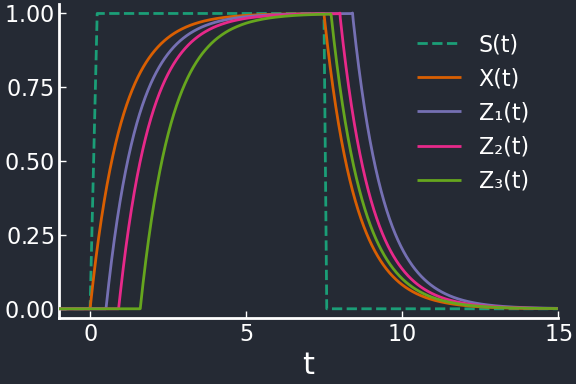
The signal \(S\) activates \(X\) which in turns activates the three genes \(Z_1, Z_2, Z_3\); the affinities \(K_Z^{(i)}\) satisfy \(K_{Z}^{(i)} < K_{Z}^{(i+1)}\) so that, when levels of \(X\) increase in response to a step in \(S\), they are activated in order. When \(S\) is turned off, \(X\) starts decaying and the target genes are deactivated inversely to their activation order. This type of program is called a LIFO (last in, first out).
FIFO temporal programs with multi-output FFLs
In many cases it might be desirable for genes to follow a FIFO order instead (first in, first out), i.e. the deactivation order is reversed with respect to the activation order. The simplest motif producing behavior is the two-output FFL.
rn = @reaction_network TwoOutputFFL_FIFO begin
(S, α), 0 ↔ X
(Θ(X,Kxy), α), 0 ↔ Y
# max acts like a OR gate here
(max(Θ(X,Kxz1),Θ(Y,Kyz1)), α), 0 ↔ Z₁
(max(Θ(X,Kxz2),Θ(Y,Kyz2)), α), 0 ↔ Z₂
end S α Kxy Kxz1 Kxz2 Kyz1 Kyz2
p = [
:S => 0.0,
:α => 1.0,
:Kxy => 0.5, :Kxz1 => 0.25, :Kxz2 => 0.75,
:Kyz1 => 0.75, :Kyz2 => 0.25
]
u₀ = [:X => 0.0, :Y => 0.0, :Z₁ => 0.0, :Z₂ => 0.0]
tspan = (-1.0, 15.0)
S_on!(integrator) = integrator.p[1] = 1.0
S_off!(integrator) = integrator.p[1] = 0.0
cb_on = PresetTimeCallback(t_on, S_on!)
cb_off = PresetTimeCallback(t_off, S_off!)
cb = CallbackSet(cb_on, cb_off)
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Rosenbrock23(), callback=cb)
plot(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="S(t)", leg=:topright)
plot!(sol, idxs=(0,1:2))
plot!(sol, idxs=(0,3:4), lab="Z".*["₁" "₂"].*"(t)")
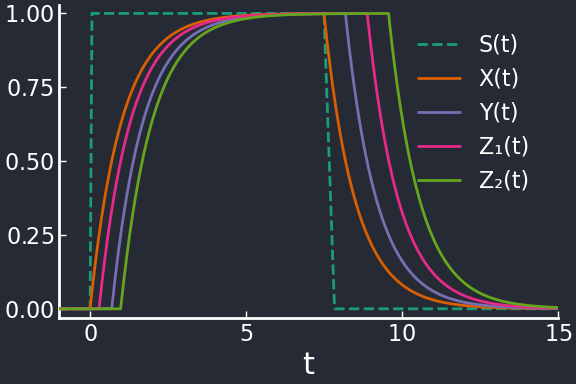
The first gene \(Z_1\) is activated first, but it is also deactivated first. This happens if the conditions \(K_{XZ_1}<K_{XZ_2}\) and \(K_{YZ_1}>K_{YZ_2}\) are satisfied. Fundamentally, thanks to the OR gate, \(X\) defines the time at which the target genes start being expressed, while \(Y\) defines the time at which they are turned off.