Feedforward loops
A brief exploration of genetic circuits via the Catalyst Julia library.
Mainly inspired by Alon, U. An introduction to systems biology: design principles of biological circuits (CRC Press, 2019).
Setup
Four packages required: Catalyst, DifferentialEquations, Plots, Latexify.
For convenience, I prepare a file (GeneticCircuits.jl) with some useful definitions; it will be assumed that this file
is always included before running any other code:
using Catalyst, DifferentialEquations, Plots, Latexify
# set a default plot style
default(
palette = :Dark2,
bgcolor = RGB(37/255, 42/255, 52/255),
thickness_scaling = 2,
grid = false,
legendfontsize = 8, legendtitlefontsize = 8,
bgcolorlegend = :transparent
)
# register heaviside function for symbolic manipulation
Θ(X,K) = X > K ? 1 : 0
@register_symbolic Θ(X,K)
Simple regulation
Simple regulatory circuits are described by the dynamics $$ \dfrac{\text{d}X}{\text{d}t} = \beta - \alpha X $$ and are trivial to represent in Catalyst:
rn = @reaction_network SimpleRegulation begin
β, 0 --> X # produce X with rate β
α, X --> 0 # degrade X with rate α
end α β
Model SimpleRegulation
States (1):
X(t)
Parameters (2):
α
β
The effect of noise on a simple regulatory circuit can be explored by introducting a time-dependent production rate \(\beta(t) = \beta_0 + \beta_1\sin(\omega t)\). We define three independent circuits:
rn = @reaction_network SimpleRegulation begin
# circuit 0: no fluctuations
β₀, 0 --> X₀
α, X₀ --> 0
# circuit 1: high-frequency fluctuations
β₀+β₁*sin(ω₁*t), 0 --> X₁
α, X₁ --> 0
# circuit 2: low-frequency fluctuations
β₀+β₁*sin(ω₂*t), 0 --> X₂
α, X₂ --> 0
end α β₀ β₁ ω₁ ω₂
p = (
:α => 1.0, # degradation rate of X
:β₀ => 1.0, # baseline production rate of X
:β₁ => 0.1, # amplitude of production rate fluctuations
:ω₁ => 5.0, # fluctuation frequency in circuit 1
:ω₂ => 0.3 # fluctuation frequency in circuit 2
)
# set initial conditions
u₀ = [:X₀ => 0.0, :X₁ => 0.0, :X₂ => 0.0];
Solving the system is now trivial via DifferentialEquations:
tspan = (0.0, 20.0)
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Tsit5())
plot(sol, leg=:bottomright)
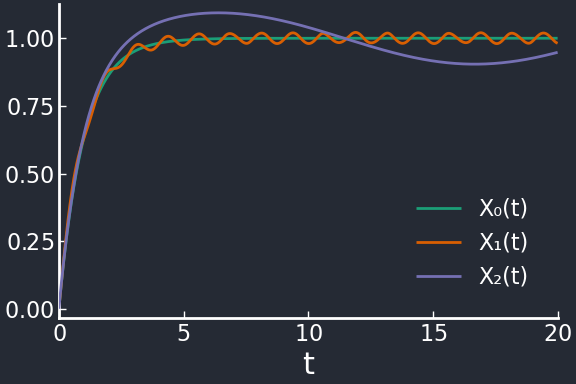
Despite having the same amplitude β₁=0.1, the fluctuations in X₁ are dampened
compared to those in X₂.
Simple regulation acts as a filter for high-frequency noise.
Feedforward loop (FFL)
The FFL is a network motif common across a wide variety of biological networks. FFLs are composed of a transcription factor \(X\) which regulates a second transcription factor \(Y\), and both of them regulate a gene \(Z\). Different combinations of activation and repression following this structure give rise to 8 possible distinct FFLs. These 8 FFLs can be subdivided into two groups: coherent and incoherent FFLs.
A FFL is coherent if the indirect regulation path from \(X\) to \(Z\) through \(Y\) has the same sign as the direct path from \(X\) to \(Z\). Viceversa, if the two paths have opposing signs the FFL is incoherent.
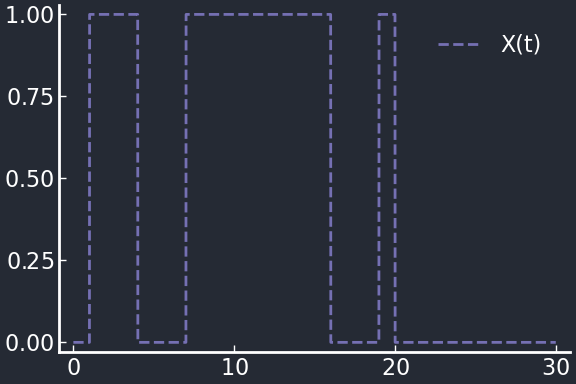
To study how FFLs work, we can imagine we are able to directly control the upstream transcription factor \(X\), modulating it in such a way to produce three step pulses of different durations.
t_on = [1.0, 7.0, 19.0]
t_off = [4.0, 16.0, 20.0]
steppulse(t,a,b) = Θ(t,a)*(1-Θ(t,b))
SX(t,t_on,t_off) = sum( map(τ -> steppulse(t,τ[1],τ[2]), zip(t_on,t_off)) )
plot(0:0.01:30.0, t -> SX(t,t_on,t_off), lc=3, ls=:dash, lab="X(t)")
For simplicity we treat activation as a logic gate: \(Y\) is activated (or deactivated) by \(X\) when \(X > K_{XY}\), \(Z\) is activated (or deactivated) by \(X\) when \(X > K_{XZ}\) and \(Z\) is activated (or deactivated) by \(Y\) when \(Y > K_{YZ}\). We also have to make the choice about how \(Z\) integrates the parallel signals from \(X\) and \(Y\). I will use an AND logic gate.
Type-1 Coherent FFL
rn = @reaction_network CoherentFFL_Type1 begin
βy*Θ(X,Kxy), 0 → Y # X → Y
βz*Θ(X,Kxz)*Θ(Y,Kyz), 0 → Z # (X → Z) AND (Y → Z)
αy, Y → 0
αz, Z → 0
end αy αz βy βz Kxy Kxz Kyz X
p = [
:αy => 1.0, :αz => 1.0,
:βy => 1.0, :βz => 1.0,
:Kxy => 0.5, :Kxz => 0.5, :Kyz => 0.75,
:X => 0.0
]
u₀ = [:Y => 0.0, :Z => 0.0]
tspan = (0.0, 30.0);
Notice that :X was set as a parameter and not as a state variable.
This will allow us to control it as we please, through the callback
interface of DifferentialEquations.jl.
X_on!(integrator) = integrator.p[end] = 1.0
X_off!(integrator) = integrator.p[end] = 0.0
cb_on = PresetTimeCallback(t_on, X_on!)
cb_off = PresetTimeCallback(t_off, X_off!)
cb = CallbackSet(cb_on, cb_off)
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Tsit5(), callback=cb)
plot(sol, leg=:bottomright)
plot!(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="X(t)")
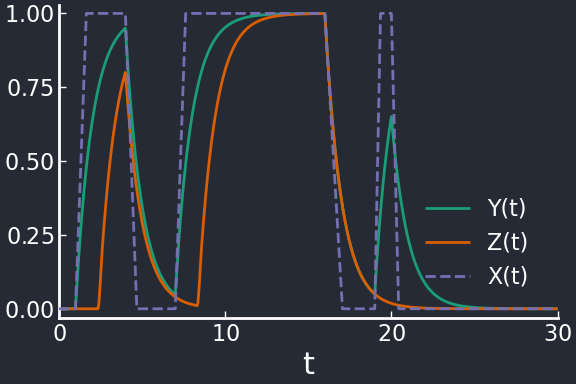
In this Type-1 Coherent FFL, all regulation paths are positive. When \(X\) is on, first \(Y\) is upregulated, but expression of \(Z\) starts only when also \(Y\) is sufficiently high (\(Y>K_{YZ}\)); this is due to the logic AND which requires both \(X\) and \(Y\) to be on for \(Z\) to be expressed. When \(X\) is turned off, both \(Y\) and \(Z\) immediately decay. If the \(X\) pulse is sufficiently long (e.g. pulse 2), both \(Y\) and \(Z\) reach a steady state, buth if the pulse is short (e.g. pulse 3), \(Y\) doesn’t have enough time to reach the threshold \(K_{YZ}\), so \(Z\) is never expressed. Summing up, this means that the Type-1 Coherent FFL is a sign-sensitive delay element: \(Z\) is expressed, with a delay, after positive pulses.
The same analysis can be performed for all other FFLs. The code is always the same, only the reaction network changes.
Type-2 Coherent FFL
rn = @reaction_network CoherentFFL_Type2 begin
βy*(1-Θ(X,Kxy)), 0 → Y # X ⊣ Y
βz*(1-Θ(X,Kxz))*Θ(Y,Kyz), 0 → Z # (X ⊣ Z) AND (Y → Z)
αy, Y → 0
αz, Z → 0
end αy αz βy βz Kxy Kxz Kyz X
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Tsit5(), callback=cb)
plot(sol, leg=:bottomright)
plot!(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="X(t)")
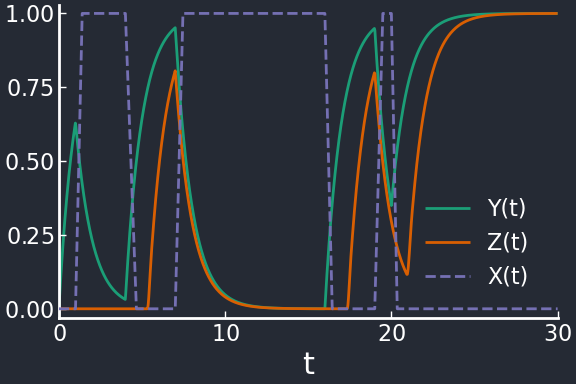
Here \(X \dashv Y \to Z\) (i.e. \(X\) indirectly represses \(Z\) by repressing \(Y\)) and \(X \dashv Z\) (\(X\) directly represses \(Z\)). When \(X\) is off, \(Y\) is promoted; only if \(X\) is off for sufficiently long times, \(Y\) can overcome the threshold \(K_{YZ}\) and promote the expression of \(Z\). This is also a sign-sensitive delay element: \(Z\) is expressed, with a delay, after negative pulses.
Type-3 Coherent FFL
rn = @reaction_network CoherentFFL_Type3 begin
βy*Θ(X,Kxy), 0 → Y # X → Y
βz*(1-Θ(X,Kxz))*(1-Θ(Y,Kyz)), 0 → Z # (X ⊣ Z) AND (Y ⊣ Z)
αy, Y → 0
αz, Z → 0
end αy αz βy βz Kxy Kxz Kyz X
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Tsit5(), callback=cb)
plot(sol, leg=:bottomright)
plot!(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="X(t)")
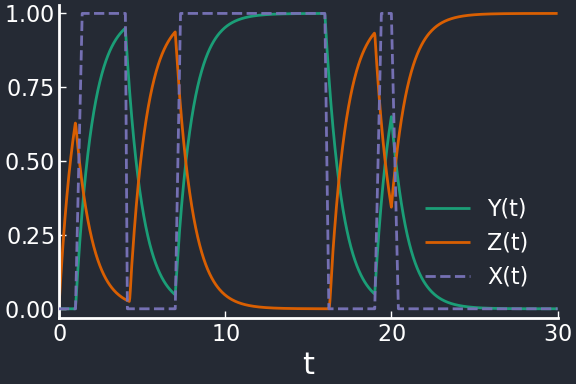
This motif produces an alternating response between \(Y\) and \(Z\). When \(X\) is turned on, \(Y\) is promoted and \(Z\) is repressed; viceversa, when \(X\) is off, \(Y\) goes down and \(Z\) is promoted. Not particularly interesting.
Type-4 Coherent FFL
rn = @reaction_network CoherentFFL_Type4 begin
βy*(1-Θ(X,Kxy)), 0 → Y # X ⊣ Y
βz*Θ(X,Kxz)*(1-Θ(Y,Kyz)), 0 → Z # (X → Z) AND (Y ⊣ Z)
αy, Y → 0
αz, Z → 0
end αy αz βy βz Kxy Kxz Kyz X
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Tsit5(), callback=cb)
plot(sol, leg=:bottomright)
plot!(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="X(t)")
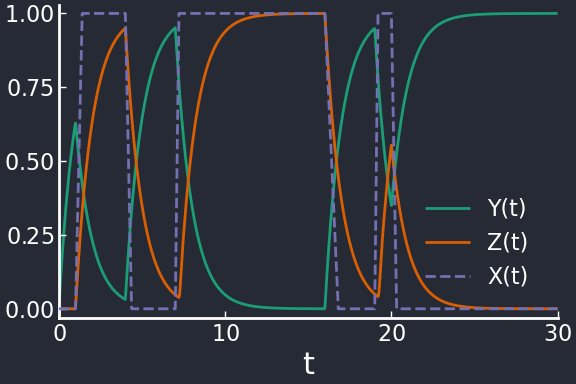
Same as the Type-3 with \(Y\) and \(Z\) inverted.
Type-1 Incoherent FFL
rn = @reaction_network IncoherentFFL_Type1 begin
βy*Θ(X,Kxy), 0 → Y # X → Y
βz*Θ(X,Kxz)*(1-Θ(Y,Kyz)), 0 → Z # (X → Z) AND (Y ⊣ Z)
αy, Y → 0
αz, Z → 0
end αy αz βy βz Kxy Kxz Kyz X
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Tsit5(), callback=cb)
plot(sol, leg=:bottomright)
plot!(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="X(t)")
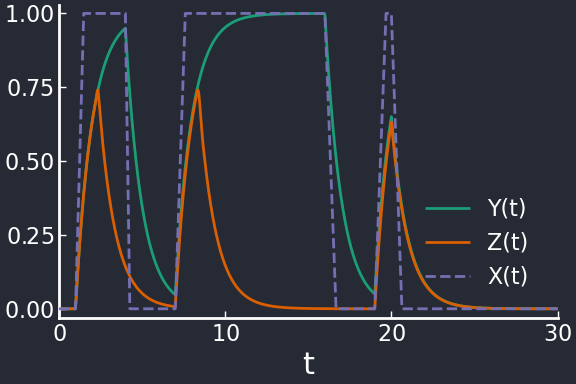
\(Y\) and \(Z\) are both directly promoted by \(X\), but when \(Y>K_{YZ}\) \(Z\) is repressed. The Type-1 Incoherent FFL produces bursts in \(Z\) after positive pulses.
Type-2 Incoherent FFL
rn = @reaction_network IncoherentFFL_Type2 begin
βy*(1-Θ(X,Kxy)), 0 → Y # X ⊣ Y
βz*(1-Θ(X,Kxz))*(1-Θ(Y,Kyz)), 0 → Z # (X ⊣ Z) AND (Y ⊣ Z)
αy, Y → 0
αz, Z → 0
end αy αz βy βz Kxy Kxz Kyz X
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Tsit5(), callback=cb)
plot(sol, leg=:bottomright)
plot!(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="X(t)")
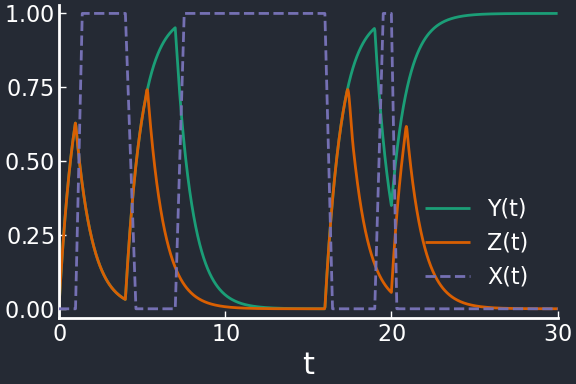
When \(X\) is off, \(Y\) and \(Z\) both increase, but when \(Y\) overcomes the threshold \(K_{YZ}\) then \(Z\) gets repressed. This motif therefore produces bursts of \(Z\) expression in response to negative \(X\) steps.
Type-3 Incoherent FFL
rn = @reaction_network IncoherentFFL_Type3 begin
βy*Θ(X,Kxy), 0 → Y # X → Y
βz*(1-Θ(X,Kxz))*Θ(Y,Kyz), 0 → Z # (X ⊣ Z) AND (Y → Z)
αy, Y → 0
αz, Z → 0
end αy αz βy βz Kxy Kxz Kyz X
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Tsit5(), callback=cb)
plot(sol, leg=:bottomright)
plot!(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="X(t)")
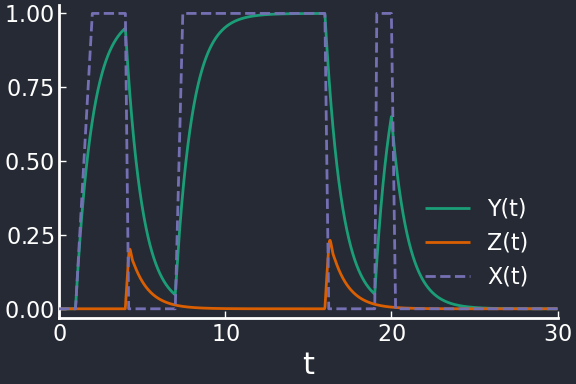
The Type-3 Incoherent FFL also produces \(Z\) bursts in response to negative \(X\) steps, but in a different way from the Type-2 Incoherent FFL. Since \(Y\) must be on to promote \(Z\), the bursts of \(Z\) only occur if \(Y\) is high enough. This means that short pulses in \(X\) (off-on-off, see pulse 3) are filtered out because \(Y\) didn’t have enough time to reach its basal level (high).
Type-4 Incoherent FFL
rn = @reaction_network IncoherentFFL_Type4 begin
βy*(1-Θ(X,Kxy)), 0 → Y # X ⊣ Y
βz*Θ(X,Kxz)*Θ(Y,Kyz), 0 → Z # (X ⊣ Z) AND (Y → Z)
αy, Y → 0
αz, Z → 0
end αy αz βy βz Kxy Kxz Kyz X
prob = ODEProblem(rn, u₀, tspan, p)
sol = solve(prob, Tsit5(), callback=cb)
plot(sol, leg=:bottomright)
plot!(sol.t, t -> SX(t,t_on,t_off), ls=:dash, lab="X(t)")
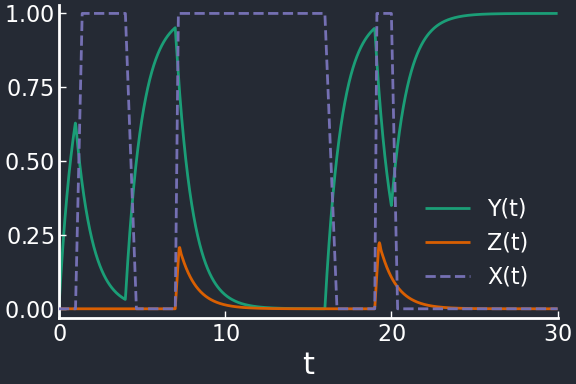
Produces \(Z\) bursts after positive \(X\) pulses, but only if \(Y\) is high enough. If \(X\) is off only for a brief interval (see e.g. at \(t=0\)), \(Y\) doesn’t increase enough to promote \(Z\) and the following positive \(X\) pulse is filtered.